Les solides qui illustrent le traité du moine Luca Pacioli intitulé De divina proportione, dont la paternité est attribuée à Léonard de Vinci, figurent parmi les dessins géométriques les plus iconiques de tous les temps. Ils ont connu une grande fortune, non seulement auprès des spécialistes, mais aussi du grand public, souvent utilisés comme éléments graphiques exploitant leur célébrité presque universelle. Jusqu’à présent, nous nous étions surtout intéressé à l’histoire de la technologie, et en particulier de la mécanique, chez Léonard de Vinci et ses contemporains. C’est en approfondissant certaines questions liées aux enjeux du dessin technique à la Renaissance que nous avons été confronté au problème de la genèse des illustrations du traité de Luca Pacioli. La bibliographie au sujet de ces illustrations est très riche, et ce à partir du xix^e siècle. Cependant, la plupart des études – comme c’est souvent le cas pour des thématiques de grand intérêt – se focalisent sur un ou plusieurs aspects particuliers. Notre contribution se fonde sur une synthèse de ces nombreuses analyses, afin de comprendre le processus d’élaboration des illustrations dans son ensemble, de déterminer leurs modalités d’exécution, et de mieux comprendre les implications de leur statut entre dessin technique et dessin artistique.

De divina proportione et Compendium de divina proportione

Lorsque l’on se réfère à l’œuvre de Luca Pacioli, il faut bien distinguer le Compendium de divina proportione, manuscrit achevé en 1498 à Milan, du De divina proportione, œuvre imprimée à Venise en 1509 chez Paganino de’ Paganini, qui comprend le Compendium1. En 1508, pendant son séjour vénitien, Pacioli présente une supplique au Sénat afin d’obtenir le permis d’imprimer cinq de ses œuvres, dont le De divina proportione2, ainsi qu’un privilège pour vingt ans empêchant quiconque de les republier à Venise pendant cette période. Il obtient le permis et se voit accorder quinze ans de privilège.

Le De divina proportione est précédé de cinq compositions poétiques et d’une lettre dédicatoire en latin adressée à Piero Soderini, gonfalonier de Florence et ami de Pacioli. Le texte du traité est divisé en trois parties autonomes. La première, le Compendium de divina proportione, concerne le rapport de proportion parfait, des polygones réguliers et l’utilisation de la perspective linéaire. La deuxième partie, intitulée Tractato de architectura, discute les idées de Vitruve sur l’application des mathématiques à l’architecture. La troisième partie, intitulée Libellus in tres partiales tractatus divisus quinque corporum regularium et dependentium, est la traduction en langue vernaculaire du traité de Piero della Francesca, le De quinque corporibus regularibus3. Enfin, l’œuvre compte un appendice de vingt-trois tables qui illustrent la construction des lettres majuscules de l’alphabet, ainsi que les célèbres gravures des polyèdres.

Le manuscrit du Compendium de divina proportione a certainement été copié au moins trois fois avant l’édition de 1509, et seuls deux exemplaires nous sont parvenus. Le premier, dédié au duc de Milan, Ludovic le More, est conservé à la Bibliothèque Publique et Universitaire de Genève (ms. Langues Étrangères n. 210). Il a été donné en 1742 par le pasteur et théologien genevois Ami Lulli, qui l’avait lui-même acheté en 1720 à Paris avec d’autres manuscrits ayant appartenu à l’antiquaire Petau. Le manuscrit de Genève est en mauvais état de conservation. Il se compose de 130 feuillets ; une enluminure représente Ludovico Sforza, assis et entouré de quatre dignitaires, en train de recevoir le livre des mains de Pacioli. Le second exemplaire copié est donné par Pacioli à Giangaleazzo Sanseverino, général du duc de Milan. Il comprend également 130 feuillets et est conservé à la Bibliothèque Ambrosienne de Milan (inv. S.P.6 ex Cod. F 170 sup.), offert le 21 janvier 1637, avec onze autres volumes, par le marquis Galeazzo Arconati4.

Les deux versions manuscrites présentent chacune de petites différences par rapport au texte imprimé du chapitre du De divina proportione, et ne sont pas non plus identiques entre elles. Dans le texte imprimé, en effet, les solides sont représentés sur 59 xylographies, tandis qu’il y en a 60 dans les deux versions manuscrites. La xylographie supplémentaire n’est pas la même dans les deux manuscrits : on trouve la « figura superflua » dans le manuscrit de Genève, et la « piramide laterata vacua » dans celui de Milan. Il convient de signaler également que la dernière des 59 xylographies du De divina proportione porte le numéro LXI. C’est pour cette raison que l’on a longtemps considéré que le traité comportait 61 planches5. Les figures suivent également un ordre différent et présentent des variations dans les dénominations : dans le traité imprimé, les noms sont en général neutres (Tetraedron, Hexaedron, Octaedron, Icosaedron, Dodecaedron), tandis que dans les manuscrits de Genève et de Milan, les noms sont en général masculins (Tetracedron, Exacedron, Octocedron, Ycocedron, Duodecedron)6. On retrouve d’autres différences encore dans les représentations des solides entre les trois versions, comme par exemple le prisme à base triangulaire (le numéro XLIII dans le manuscrit de Genève) que l’on trouve sous ses formes solides et vides : dans le manuscrit de Genève, le polyèdre solide montre frontalement un angle, tandis que la version vide présente une face plate ; dans le manuscrit de Milan, au contraire, dans les deux cas, le polyèdre montre frontalement une face plate ; enfin, dans l’édition de 1509, le solide est représenté de manière analogue au manuscrit de Genève, mais la forme solide est retournée de bas en haut, comme si le point de vue de l’observateur se trouvait plus en contrebas du solide. On retrouve les mêmes différences pour la « piramide laterata triangola ».

Signalons que, dans la version éditée, certaines figures sont retournées de gauche à droite, comme dans le cas de la « piramide laterata triangola inequilatera » dans sa forme vide. Ce genre de retournement pourrait être dû au processus de reproduction de la xylographie, mais, alors, nous devrions observer le même phénomène pour toutes les figures gravées, ce qui n’est pas le cas.

Si l’on considère les nombreuses différences entre le codex de Genève, celui de la Bibliothèque Ambrosienne et l’édition de Venise de 1509, la plupart des historiens sont d’accord sur le fait que cette dernière n’a pas été réalisée à partir de l’un des manuscrits qui nous sont parvenus, mais à partir d’un troisième, aujourd’hui perdu. Celui-ci aurait été offert par Pacioli à son ami Pietro Soderini, gonfalonier de Florence, ce qui serait cohérent avec la dédicace du volume imprimé7.

Les soixante-et-onze chapitres qui composent le Compendium sont divisés en quatre sections, dont le contenu, le style mathématique et la typologie des illustrations accompagnant le texte, sont assez distincts.

La première section revêt un caractère philosophique et théologique : Pacioli propose d’insérer la perspective dans les disciplines mathématiques en vertu de son utilisation pour les proportions8.

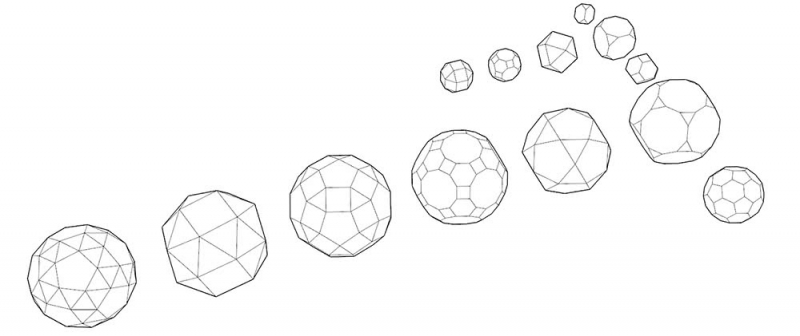
La deuxième section est une traduction en langue vernaculaire du xiii^e livre des Éléments d’Euclide, dont l’auteur ne reproduit que quelques démonstrations de théorèmes, illustrées à l’aide de schémas géométriques analogues à ceux de l’édition de Johannes Campanus9. Parmi ces démonstrations, on trouve les propositions présentant treize propriétés, ou « effets » remarquables, relatifs à la « division d’un segment en moyenne et extrême raison », que nous appelons aujourd’hui « section dorée10 » et que Pacioli appelle « divine proportion11 ». La suite de la section s’occupe de la construction des « corps réguliers » à partir du diamètre de la sphère qui les contient. Il s’agit de cinq polyèdres réguliers et convexes, qui ont pour faces des polygones réguliers identiques entre eux et qui ont tous les angles et les sommets égaux (tab. 1 et fig. 1).

Tab. 1 : Les cinq polyèdres réguliers (platoniciens).

	faces triangulaires	faces carrées	faces pentagonales
tétraèdre	4
hexaèdre (ou cube)		6
octaèdre	8
dodécaèdre			12
icosaèdre	20

Dans l’Antiquité, ces solides ont suscité l’intérêt des savants pour leurs propriétés, dont certaines sont justement liées à la « section dorée ». D’ailleurs, Euclide conclut ses Éléments, après avoir construit les cinq polyèdres réguliers, en démontrant qu’il ne peut y avoir d’autres configurations polyédriques régulières hormis les cinq déjà connues12. Il en est de même pour Pacioli qui, après les avoir décrits et en avoir déterminé les côtés en fonction du diamètre de la sphère circonscrite, démontre que les polyèdres réguliers ne sont qu’au nombre de cinq, et précise comment et quand l’un d’eux peut être inscrit dans un autre. Pacioli reprend ensuite la conception platonicienne des éléments décrite dans le Timée13, où les cinq polyèdres réguliers sont considérés comme des symboles de l’univers et de ses éléments de base : le feu (le tétraèdre), la terre (le cube), l’air (l’octaèdre) et l’eau (l’icosaèdre). Le dodécaèdre symbolise la quintessence qui entoure tout et comprend tout en son sein : il s’agit d’une métaphore qui trouve une correspondance sur le plan mathématique parce qu’il est possible de démontrer qu’il est justement le seul polyèdre régulier dans lequel on peut inscrire les quatre autres. Il est également associé à l’image de l’univers entier et de la perfection parce qu’il est le polyèdre qui s’approche le plus de la forme sphérique14. Pour Pacioli, donc, comme pour Platon, la nature est composée de cinq éléments « bastants et suffisants » à satisfaire « le besoin naturel » de telle sorte qu’il « ne manque au besoin et ne l’excède pas15 ». Le fait que l’univers soit composé de seulement cinq éléments trouve une correspondance parfaite dans la démonstration géométrique que les polyèdres réguliers sont au nombre de cinq : de même qu’il n’existe d’autre polyèdre régulier outre le tétraèdre, l’octaèdre, le cube, l’icosaèdre et le dodécaèdre, de même il n’existe d’autre élément dans la nature que le feu, l’air, la terre, l’eau et la quintessence.

Dans la troisième section du Compendium, Pacioli s’occupe de certains polyèdres semi-réguliers qui, comme les polyèdres réguliers, sont en nombre fini : treize figures déterminées au iii^e siècle av. J.-C. par le mathématicien de Syracuse, Archimède, d’où leur appellation de solides « archimédiens ». Il s’agit de polyèdres convexes qui présentent certaines des caractéristiques de régularité des cinq solides platoniciens, mais pas toutes : les faces de ces polyèdres sont des polygones réguliers, mais pas toujours du même type (fig. 2). En outre, les sommets doivent se correspondre, c’est-à-dire que les faces doivent être disposées dans le même ordre autour d’un même sommet.

Deux de ces solides sont chiraux, et ne sont donc pas équivalents à leur image reflétée : pour cette raison, dans certains contextes, ces polyèdres sont considérés deux fois, arrivant ainsi à quinze solides archimédiens. Les treize solides archimédiens sont les suivants :

Tab. 2 : Les treize polyèdres semi-réguliers (archimédiens).

	faces tri-angulaires	faces carrées	faces penta-gonales	faces hexa-gonales	faces octo-gonales	faces déca-gonales
tétraèdre tronqué	4			4
octaèdre tronqué		6		8
cuboctaèdrea	8	6
rhombicuboctaèdre	8	18
icosaèdre tronqué			12	20
icosidodécaèdre	20		12
cube tronqué	8				6
cuboctaèdre tronqué		12		8	6
dodécaèdre tronqué	20					12
icosidodécaèdre tronqué		30		20		12
rhombicosidodécaèdre	20	30	12
cube adouci (ou cuboctaèdre adouci), polyèdre chiral	32	6
dodécaèdre adouci, polyèdre chiral	80		12
a. Pacioli l’appelle « cube tronqué », nom que l’on donne aujourd’hui à un autre solide semi-régulier (voir plus bas dans le tableau).

Pacioli définit ces solides comme « dépendants », car ils sont obtenus en tronquant d’autres figures, processus pour lequel on enlève certaines parties à un solide de manière à en obtenir un nouveau qui respecte les caractéristiques de régularité demandées. Dans le cas des polyèdres semi-réguliers plus complexes, cette procédure représente une grande simplification17, à tel point que Pacioli, dans son De divina proportione, ne s’occupe que des six premiers solides de la liste ci-dessus18.

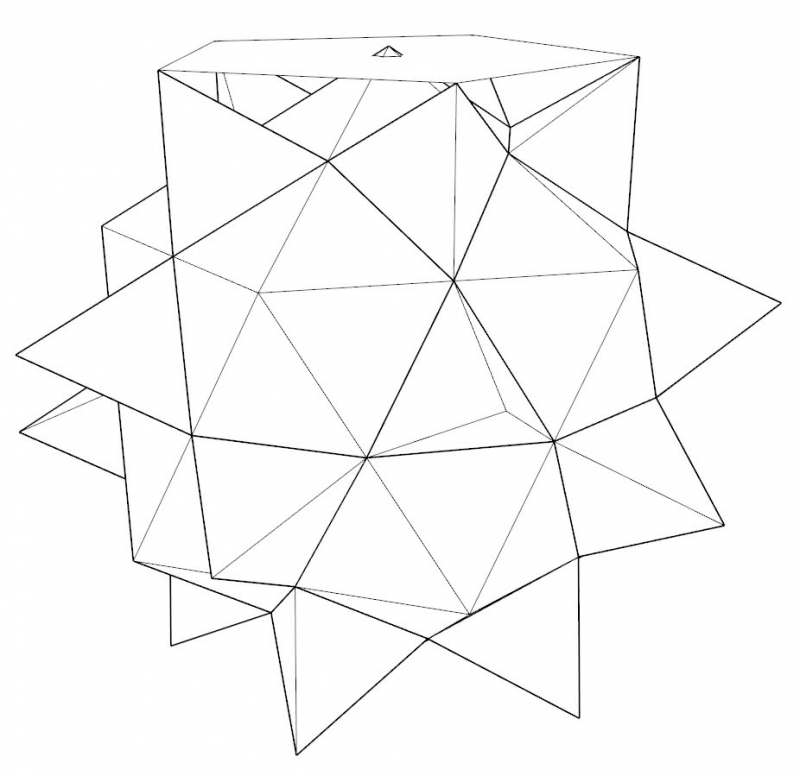
À partir de ces 6 solides et des 5 solides réguliers, Pacioli construit leur dérivé par stellation, procédé qui prévoit la substitution de chaque face du polyèdre par une pyramide qui a comme base une face et, pour les autres faces, des triangles équilatéraux (fig. 3). Dans le langage du De divina proportione, un solide obtenu en le tronquant est dit « abscis », tandis qu’un solide obtenu par stellation est dit « élevé ».

La quatrième partie du Compendium est composée de planches relatives aux « corps oblongs », c’est-à-dire aux pyramides, cônes et parallélépipèdes, dont Pacioli fournit, dans le style des abaques, les formules permettant de calculer leurs superficies et leurs volumes, en fournissant quelquefois un exemple numérique particulier.

D’un point de vue stylistique, l’œuvre de Pacioli est composée de deux parties nettement distinctes. Dans la première, les dessins servent de support au texte et sont plutôt classiques, comme ceux de l’œuvre de Johannes Campanus de Novare19 ou de l’édition princeps d’Erhard Ratdolt20 : des schémas géométriques qui illustrent les démonstrations des théorèmes contenus dans le XIII^e livre des Éléments d’Euclide. La seconde partie, qui traite des solides platoniciens et archimédiens, ne contient aucune démonstration mathématique, mais fournit une simple description des polyèdres. Ceux dits « semi-réguliers », en particulier, sont présentés par une simple liste du nombre de côtés, des angles « superficiels et solides » et des bases qui les constituent. Les 60 planches (59 dans l’édition de 1509) représentent les polyèdres, à la fois dans leur forme « solide », c’est-à-dire avec les faces pleines, et dans leur forme « vide », dans laquelle seuls les sommets sont représentés. Le résultat rappelle quelque peu la modalité de visualisation que l’on appelle « wireframe » dans les programmes modernes de modélisation tridimensionnelle.

Chaque fois que l’un des polyèdres est décrit, un chiffre romain en marge du texte renvoie à la planche correspondante. C’est Pacioli lui-même qui explique au lecteur comment rapporter ces chiffres aux planches qui concluent l’œuvre : il lui demande de rechercher, dans la marge du texte, le chiffre romain correspondant au numéro du chapitre en question, auquel est joint la lettre de la planche citée en exemple (par exemple : I.e ; III.a, etc.). Il lui dit également que la figure correspondante est réalisée sur la surface plane en perspective « comme le sait bien Léonard de Vinci », et que, juste au-dessus des formes matérielles, se trouve leur nom en grec et en latin21. Il n’existe pas de tradition iconographique à laquelle on puisse reconduire cette partie de l’œuvre de Pacioli.

Le Libellus de quinque corporibus regularibus de Piero della Francesca22, que Pacioli traduit en langue vulgaire et inclut dans le De divina proportione, présente des dessins de projections orthogonales et des axonométries des polyèdres afin d’illustrer des problèmes de stéréométrie23. Les planches n’ont pas l’objectif d’aider le lecteur à suivre les passages de démonstrations ou d’illustrer des problèmes. Il s’agit plutôt de matérialisations de formes abstraites, dont l’ajout de couleurs contribue à un naturalisme sans précédent, tant et si bien que Pacioli lui-même affirme de vouloir présenter aux yeux du lecteur des « formes jusqu’à présent cachées aux vivants24 ».

Luca Pacioli et Léonard de Vinci

Entre 1496 et 1499, Luca Pacioli se trouve à Milan, titulaire d’un enseignement de mathématique créé exprès pour lui par Ludovic le More. Dans la lettre dédicatoire à ce dernier, au début du Compendium, il cite quelques illustres personnages qui fréquentent la cour des Sforza en février 1498 : Ambrogio Rosa, Alvise Marliano, Gabriele Pirovano, Nicola Cusano, Andrea Novarese. Il cite également Léonard de Vinci et évoque son monument équestre à Francesco Sforza, le père de Ludovic, jamais achevé25. Il précise les mesures et le poids du bronze, avant de mentionner sa Dernière Cène à Santa Maria delle Grazie, un traité de sa main sur la peinture, ainsi qu’une autre « œuvre inestimable sur le mouvement local, les percussions et poids de toutes les forces26 ». On sait que Pacioli, en plus de collaborer avec Léonard de Vinci, entretient avec lui un lien étroit d’amitié et d’estime réciproque, qui perdure jusqu’à leur voyage ensemble, après avoir quitté Milan, à Ferrare, Venise et Florence27.

En retour, Léonard de Vinci lit et étudie les œuvres de Pacioli, approfondissant ainsi ses connaissances mathématiques. Au folio 288r. du Codex Atlanticus, daté de 1495 environ, Léonard annote ainsi la dépense considérable de « 119 in Aritmetrica di maestro Luca28 » c’est-à-dire pour l’acquisition de la Summa de arithmetica, geometria, proportioni et proportionalita, publiée par Pacioli en 149429. Le même volume est cité au folio 3r. du Codex de Madrid II, dans une longue liste de livres laissés « enfermés dans un coffre » et « dans un coffre au monastère », le monastère en question étant probablement Santa Maria Novella à Florence, où Léonard résidait en 1503 tandis qu’il travaillait à la Bataille d’Anghiari30. Une autre note du Codex Atlanticus, datant à peu près de la même époque indique, parmi une liste de choses à faire, que Léonard doit « apprendre la multiplication de la racine de Maître Luca31 ».

Il est probable que Pacioli ait donné à Léonard de véritables leçons, étant donné que ce dernier pouvait difficilement apprendre directement des textes qui sont principalement en latin. En contrepartie, Léonard offre à Pacioli ses propres compétences artistiques, en dessinant les originaux des solides du Compendium de divina proportione que Pacioli termine en 1498.

C’est Pacioli qui nous informe que les dessins ont été réalisés par Léonard de Vinci. On peut lire dans le Compendium que chaque polyèdre est « fait en plan avec toute perfection de perspective, comme le sait notre Léonard de Vinci32 », et, dans le Tractato del’architectura, que les figures sont « de la main de notre apprécié compatriote Léonard de Vinci florentin33 ». On trouve une autre référence explicite dans la lettre dédicatoire d’un manuscrit de Pacioli intitulé De viribus quantitatis, dans lequel il mentionne :

[les] suprêmes et très gracieuses figures de tous les corps réguliers et dépendants platoniciens et mathématiques, qu’il n’est pas possible au monde de mieux dessiner en perspective […] faites et formées par cette ineffable main gauche très habituée à toutes les disciplines mathématiques, du prince parmi les mortels, florentin d’abord, notre Léonard de Vinci en ces temps heureux que nous avons passés ensemble dans la très admirable ville de Milan34.

Par ailleurs, dans l’œuvre de Léonard de Vinci aussi il y a de clairs indices du travail réalisé pour Pacioli. On trouve, par exemple, dans le Codex Atlanticus, des dessins et des esquisses de solides. On voit en particulier, aux folios 707r. et 708r. (fig. 4-5), deux représentations de l’icosidodécaèdre, dans ses versions solide et « vide », correspondant exactement à celles du « Duodecedron abscisus solidus » et du « Duodecedron abscisus vacuus » des planches XXIX et XXX du Compendium35 (fig. 6-7).

Les illustrations du Compendium

Même si tous les chercheurs ne sont pas d’accord pour l’attribution à Léonard de ces dessins du Codex Atlanticus36, leur correspondance avec les planches du Compendium est indéniable37. En outre, au folio 80v. du manuscrit M de l’Institut de France (fig. 8), on trouve un tercet que Léonard définit comme « Tercet fait pour les corps réguliers et leurs dérivatifs », qui est quasiment le même que celui qui ouvre le De divina proportione :

El dolce frutto, vago e sì diletto
constrinse già filosafi cercare
causa di noi per pascere lo ‘ntelletto38.

Sous le tercet sont dessinées les figures des cinq polyèdres réguliers. Notons également que ces figures sont dotées d’un commentaire utilisant les termes de tetracedron, eusacedron, duodecedron, ottocedron, icocedron, qui se rapprochent plus de ceux utilisés dans le manuscrit du Compendium que de ceux utilisés dans l’œuvre successive imprimée39.

Même s’il ne semble pas y avoir de doute sur la paternité des dessins du Compendium, il reste un sujet qui a longuement été débattu : la méthode avec laquelle les dessins ont été réalisés. En effet, il y a deux possibilités : soit Léonard de Vinci a construit des perspectives mathématiquement exactes des polyèdres à partir des principes de la géométrie euclidienne, en employant des projections, soit il a réalisé des modèles tridimensionnels réels dans une perspective empirique, à l’aide d’un quelconque instrument.

L’hypothèse la plus largement admise est celle selon laquelle Léonard de Vinci aurait dessiné en perspective des modèles physiques construits par Pacioli, qui aurait ensuite conservé les dessins originaux de l’artiste et les aurait recopiés dans les manuscrits du traité. C’est ce que semble témoigner un passage du De viribus quantitatis, dans lequel Pacioli raconte comment Léonard de Vinci « avec une grande force fit dans ledit livre de sa glorieuse main les corps mathématiques que nous conservons encore et qui émerveillent tous ceux qui les admirent40 ».

En revanche, il ne subsiste aucun doute sur le fait que Pacioli ait effectivement construit des modèles des polyèdres. Il déclare dans le Compendium avoir déjà fabriqué des modèles de corps réguliers et d’autres « qui en dépendent » pour Pietro Valetari, en 1489, tandis qu’il se trouvait à Rome41. Il évoque ensuite la réalisation de trois séries de polyèdres, de 60 exemplaires chacune, pour les dédicataires des copies du Compendium et du De divina proportione. La première série remonte à la période milanaise, comme en témoigne la mention de « formes colorées et décorées » pour Ludovico Sforza, dont Pacioli regrette la modeste réalisation : « lesquelles non de vil matière (comme j’en ai été forcé par pauvreté), mais mériteraient d’être ornés de précieux métal et de fines gemmes42 ». La deuxième série a également été fabriquée à Milan, pour Giangaleazzo Sanseverino et, la troisième, à Florence, pour son ami gonfalonier Pietro Soderini :

Et les formes desdits corps matériels, très belles, avec beaucoup d’élégance, je les ai disposées de mes propres mains ici à Milan, colorées et décorées et elles furent au nombre de 60 entre régulières et dépendantes. Et de même, j’en ai disposé autant pour mon patron le seigneur Galeazzo Sanseverino dans ce même lieu. Et ensuite autant à Florence pour notre gonfalonier perpétuel Petro Soderino, qui se trouvent à présent dans son palais43.

On trouve la confirmation de cette dernière information dans le paiement de 52 lires et 9 sous que Pacioli reçoit de la Seigneurie de Florence le 30 août 1502 pour « plusieurs corps géométriques44 ».

L’idée de construire des modèles matériels de polyèdres à usage didactique n’est par ailleurs pas une nouveauté : on la trouve déjà chez Campanus. Le commentateur d’Euclide, en effet, réfléchissant sur l’opportunité ou non de dessiner en marge du texte des figures tridimensionnelles des solides, relève que :

Il n’est pas approprié d’exécuter des représentations en plan, et pour cela il reste ferme que ce qui est dit, tu le conçoives avec l’esprit et que la même chose tu la complètes avec l’action et la mise en œuvre45.

La même idée apparaît aussi dans le De arte mensurandi (vers 1344) de Johannes de Muris46. L’auteur, en effet, doute de la possibilité d’imaginer les polyèdres et raconte comment lui-même a projeté des modèles, réalisés ensuite par un tailleur de pierre :

Il se peut que l’imagination ne soit pas suffisante pour se représenter de tels corps, pour cela je conseille de réaliser matériellement les 5 solides réguliers, comme je l’ai fait moi-même, en les traçant, pour les faire fabriquer ensuite en pierre par un tailleur, en ma présence, de manière qu’il [le tailleur] ne soit pas induit en erreur par la multitude des lignes. Ainsi, ce jour-là, l’habileté et l’intelligence ont collaboré de pair, comme de vrais amis47.

Peut-être a-t-on une trace de la réalisation effective des modèles de Pacioli dans le célèbre Portrait de Luca Pacioli et de son élève (1495), attribué à Jacopo de’ Barbari et conservé au Musée de Capodimonte à Naples (fig. 9). Pacioli y est représenté tandis qu’il illustre un des théorèmes d’Euclide à un jeune homme à côté de lui, souvent identifié comme étant Guidobaldo da Montefeltro, à qui est dédiée la Summa. Dans le tableau, on voit, justement posé sur un exemplaire de cette œuvre, un modèle en bois du dodécaèdre, ainsi qu’un rhombicuboctaèdre transparent accroché en haut à gauche, partiellement rempli d’eau. L’artiste a peint, de manière remarquable, l’image d’une architecture – vraisemblablement le palais ducal d’Urbino – reflétée et réfractée sur les faces du polyèdre. Ajoutons également que Bernardino Baldi, à la fin du xvi^e siècle, dans ses Vite de’ matematici, fait référence à une œuvre de Piero della Francesca, conservée dans la « garde-robe de nos sérénissimes Princes d’Urbino », représentant :

[le] portrait au naturel du frère Luca, avec son livre devant la Somma Aritmetica et quelques corps réguliers feints en cristal accrochés en haut, grâce auxquels, de par leurs lignes, et de par les lumières et de par les ombres, on découvre combien Piero était expert en sa profession48.

Enfin, on découvre sans surprise que Pacioli donne lui-même, dans le De divina proportione, un procédé pour la réalisation matérielle des polyèdres, précisant comment « dans la sphère s’insèrent tous les cinq corps réguliers49 ». Celui-ci est le même pour tous les cinq polyèdres réguliers : il faut trouver les points qui déterminent les lignes de coupe. Les indications de Pacioli pourraient être données telles quelles à des tailleurs de pierre qui, d’après le mathématicien, n’avaient pas les connaissances nécessaires pour réaliser en autonomie des formes complexes. Il raconte à ce sujet un épisode dans lequel un des sculpteurs qui travaillent pour le comte Girolamo Riario est victime d’un piège que lui tend l’auteur. En effet, ce dernier convainc le comte de proposer au pauvre sculpteur de tailler un polyèdre semi-régulier :

[…] du temps du chantier du palais du feu comte Girolamo à Rome, […] pour le plaisir de la spéculation nous exhortons […] le comte de faire faire un certain chapiteau dans une de ces formes, sans lui expliquer la difficulté mais en lui disant juste qu’il s’agissait d’une chose digne et sérieuse.

Le tailleur engagé par le comte est sûr de réussir l’entreprise assurant qu’il s’agit d’une « petite affaire et qu’il en avait fait plusieurs fois […] ». Il gâcha beaucoup de marbre. À la fin, le comte ne l’oblige à rien d’autre qu’à rembourser les pierres, mais, vexé de l’injure, il demande au mathématicien de lui enseigner comment procéder, ce qu’il fait pendant plusieurs jours à Rome50. Pacioli conclut, à propos des « lapicides » qu’ils « ne savent ni ne veulent apprendre » et qu’il s’est amusé ainsi de leur ignorance51.

Revenons aux dessins du De divina proportione. Il est donc tout à fait possible que Léonard de Vinci ait pu les réaliser en ayant devant lui des modèles de polyèdres, et tous les chercheurs pensent presque unanimement qu’il les a copiés en utilisant un instrument de perspective. Ces instruments ont commencé à se développer peu après la démonstration de la tavoletta de Brunelleschi. Grâce à eux, les peintres arrivent désormais à reproduire la réalité visuelle en perspective sur une feuille de papier.

Dans son De Pictura52, Leon Battista Alberti décrit un système d’aide à la reproduction des images en perspective qui prévoit de dessiner les objets sur une « grille », c’est-à-dire une surface ponctuée de lignes directrices et placée perpendiculairement à la directrice qui unit le centre de la surface à l’objet à reproduire. Alberti parle d’un « voile très fin, tissu rare, teinté de la couleur qui te plaira, qui se démarque par des fils parallèles plus gros au nombre qui te plaît ; il s’agit d’un instrument que mes amis et moi appelons intersection53 ».

Pacioli aussi rapporte l’utilisation de ce type d’instrument. Dans son Trattato d’architettura, il rédige deux chapitres qui, même s’ils traitent d’architecture, comprennent des considérations théoriques et pratiques concernant le travail des peintres : Pacioli y décrit l’utilisation de la « grille » pour réaliser une image correcte54. Il semble toutefois improbable que Pacioli ait décrit cet instrument parce qu’il en a fait personnellement l’usage. Il est bien plus probable qu’il ait observé son maniement chez d’autres personnes, comme chez Léonard de Vinci qui traite dans divers passages du manuscrit A de l’Institut de France de l’utilisation de cet instrument pour dessiner des images en perspective et qui suggère de les employer comme auxiliaires pour dessiner la figure humaine :

La perspective n’est autre chose que voir quelqu’un assis derrière une vitre plane et bien transparente, sur laquelle on dessine toutes les choses qui sont vues derrière la vitre, choses que l’on peut déduire par des pyramides partant de l’œil, et ces pyramides se coupent sur ladite vitre55.

La paroi est une ligne perpendiculaire, laquelle se trouve devant le point commun, où se rejoignent les pyramides ; et cette paroi fait avec ce point le même office que ferait la vitre plane à travers de laquelle tu regarderais diverses choses et que tu les y dessinais. Et les choses dessinées seraient plus petites qu’à l’origine, c’est-à-dire que ce qui est entre la vitre et l’œil serait 10 fois plus petit que ce qui est entre la vitre et la chose56.

Manière de dessiner un paysage d’après le naturel, ou de faire un plan exact de quelque campagne. Ayez un carreau de verre bien droit, de la grandeur d’une demi-feuille de grand papier, et le posez bien à plomb et ferme entre votre vue et la chose que vous voulez dessiner, puis éloignez-vous du verre à la distance des deux tiers de votre bras, c’est-à-dire, d’environ un pied et demi, et par le moyen de quelque instrument, tenez votre tête si ferme, qu’elle ne puisse recevoir aucun mouvement ; après, couvrez-vous un œil ou le fermez, et avec la pointe d’un pinceau ou d’un crayon, marquez sur le verre ce que vous verrez au travers, et contre-tirez au jour sur du papier ce qui est tracé sur le verre ; enfin calquez ce dessin qui est sur le papier, pour en tirer un autre plus net sur un nouveau papier, vous pourrez mettre en couleur ce dernier dessin, si vous voulez ; mais ne manquez pas d’y observer la perspective aérienne57.

Tous ces passages semblent se matérialiser dans le dessin du folio 5r. Du Codex Atlanticus58, dans lequel l’artiste est immortalisé tandis qu’il utilise un perspectographe, système analogue en substance à la grille, afin de représenter une sphère armillaire. Les sphères armillaires, ainsi que d’autres objets aux formes géométriques variées, font partie des sujets qui apparaissent fréquemment dans les marqueteries de l’époque, ce qui montre que Léonard de Vinci n’a certainement pas été ni le premier ni le seul à utiliser de tels instruments pour faciliter et accélérer cet exercice ardu de la projection en perspective.

Dans une de ses études qui analyse les différents éléments qui tendent à démontrer la thèse selon laquelle Léonard de Vinci aurait employé un perspectographe ou un système analogue pour dessiner les solides de Pacioli, Martin Kemp montre comment, en tentant de dessiner avec précision un corps complexe comme une sphère armillaire ou un solide archimédien, l’utilisation de la vitre aurait représenté une grande aide ainsi qu’une grande économie de temps par rapport à la méthode de la géométrie projective59. En effet, dans les folios de Léonard de Vinci, il n’y a aucune trace des constructions géométriques de ces figures60, alors qu’il en existe pour d’autres : on voit par exemple au folio 706r. du Codex Atlanticus61 le dessin articulé d’un solide pseudo-cylindrique qui est perforé selon la technique commune permettant d’obtenir les deux moitiés du dessin parfaitement symétriques62.

Il y a un autre élément qui plaide pour un « portrait » d’après nature des solides illustrant le Compendium : c’est le changement continuel de point de vue entre les planches. Pendant le travail, Léonard de Vinci a pu ajuster « à l’œil », d’une planche à l’autre, l’orientation des solides, à la recherche d’un point de vue qui illustre le mieux toutes les caractéristiques des solides63. En outre, toujours en faveur de cette hypothèse, même dans la diversité des points de vue, toutes les figures sont éclairées – de manière très naturaliste – par une source de lumière placée en haut à droite, ce qui permet aux pyramides des corps « élevés » d’avoir des faces ombrées à l’opposé de la source lumineuse, et de projeter leur ombre sur les autres faces du polyèdre64.

La seconde phase de la réalisation des planches du Compendium, une fois réalisés les dessins des modèles en bois que Pacioli a fait fabriquer, a certainement été de préparer des cartons permettant, grâce à la technique du « spolvero », de reproduire les dessins dans le codex de la Bibliothèque Ambrosienne et dans celui de Genève. Le premier des deux manuscrits – tous deux de la main du copiste Giovanni Battista Lorenzi – contient les meilleures copies des dessins de Léonard de Vinci, qui pourrait être intervenu personnellement sur ce manuscrit pour réaliser les planches des polyèdres les plus complexes, en particulier pour les finitions du dessin. Martin Kemp et Pietro Marani sont de cet avis : ils soulignent tous deux le rendu quasi pictural de bon nombre de dessins de l’exemplaire de Milan, qui présentent, de surcroît, dans certains cas, des traces de très fins traits de gaucher dans les zones d’ombre65.

La contribution de Pietro Marani fait office de référence concernant les hypothèses sur la technique de réalisation des illustrations des versions manuscrites et de celle imprimée : d’après cet auteur, les dessins ont été créés à chaque fois ad hoc sur la base de ceux de Léonard de Vinci. Il était habituel de transposer les dessins en utilisant des cartons, afin d’obtenir des bases pour la peinture ou de simples copies66. Ce système permettait de dupliquer, de varier ou de corriger un dessin original, non seulement dans le cas de compositions artistiques plus traditionnelles, mais aussi dans le cas de dessins « scientifiques ». C’est le cas par exemple de l’étude du mazzocchio, le célèbre couvre-chef florentin, au folio 710r. du Codex Atlanticus67 (assez similaire au dessin du f. 706r.), qui a été perforée son seulement pour dupliquer et transférer le dessin, mais aussi pour obtenir une symétrie exacte dans les deux moitiés de l’image.

D’après Marani, les deux icosaèdres déjà cités, aux f. 707r. et 708r. du Codex Atlanticus, seraient les deux seuls survivants d’une série plus grande qui comprenait cinquante-huit autres modèles. Réalisés à la plume, les deux dessins présentent des traces de points de poudre le long des lignes de bordure, et ne sont pas eux-mêmes troués, ce qui prouve qu’ils sont le résultat d’un transfert à partir d’un original. Ils ont pu être réalisés afin de préserver une copie des originaux, destinés à s’abîmer en raison des poudrages successifs. Marani note à ce sujet que tant les dessins du Codex de Milan que ceux du Codex de Genève présentent ces traces de poudre. Nous pouvons également avancer une autre hypothèse : il pourrait s’agir de copies réalisées dans l’objectif d’être décalquées sur des feuilles de parchemin suffisamment fines pour pouvoir les voir en transparence lorsqu’elles sont placées en dessous, ce qui est bien le cas des feuilles de parchemin du manuscrit de Genève. Ajoutons également que beaucoup de lignes sont tracées à main levée et que leur dimension correspond presque parfaitement à celle des dessins originaux des deux manuscrits du De divina proportione68. En outre, les xylographies de l’édition de 1509, dont les nombreux passages pour arriver du dessin original à celui imprimé peuvent avoir provoqué de légères altérations de dimensions, sont de la même taille que ceux du Codex Atlanticus.

Marani note aussi que le point de vue du « Dodecaedron abscissum solidum » (pl. XXIX) de l’édition est différent de celui des illustrations correspondantes des deux manuscrits. Si l’on exclut la possibilité qu’il s’agisse d’une altération du dessin due au processus de réalisation de la xylographie, on pourrait suggérer l’existence d’autres dessins originaux pris de divers points de vue, différents de ceux utilisés dans les deux versions manuscrites.

À propos des xylographies de la version éditée, signalons qu’il y a eu un débat au sujet de leur paternité dès le début du xx^e siècle : plusieurs chercheurs ont défendu — et défendent — l’opinion qu’elles seraient de facture trop grossière pour être de la main de Léonard de Vinci. D’autres chercheurs ont soutenu le contraire, sur la base d’une déclaration de Pacioli lui-même, contenue dans la lettre dédicatoire à Pietro Soderini : il affirme avoir ajouté au Compendium de divina proportione offert à Ludovic le More les « schemata quoque sua Vincii nostri Leonardi manibus scalpta », c’est-à-dire les figures gravées des mains de Léonard de Vinci. La formule « scalpta » a été interprétée justement par ces derniers chercheurs dans le sens de « gravés » dans le bois, tandis que les premiers lui attribuent un sens plus générique, celui de « tracés »69.

Même s’il semble que l’on puisse exclure une construction géométrique pour les figures du De divina proportione, l’intérêt de Léonard de Vinci pour les polyèdres, né de sa rencontre avec Pacioli et de la réalisation des planches pour illustrer son œuvre, ne se limite pas à l’exécution des modèles en bois. La méthode que Pacioli emploie pour obtenir, à partir des solides réguliers, des solides semi-réguliers, consiste à couper à la moitié ou au tiers les pointes du polyèdre original70. Par exemple, le dodécaèdre « abscis » (appelé aujourd’hui icosidodécaèdre), s’obtient en coupant à moitié les côtés du dodécaèdre original. C’est exactement ce que l’on voit dans les dessins de Léonard de Vinci qui se trouvent aux folios déjà cités 707r. et 708r. du Codex Atlanticus, dans leur forme solide et vide. De plus, le folio 735v. du Codex Atlanticusf.71 contient les dessins de 9 polyèdres semi-réguliers et montre les passages nécessaires pour les obtenir : on trouve aussi parmi eux le dodécaèdre « abscis », que Léonard de Vinci obtient justement en coupant à moitié les côtés d’un dodécaèdre. La même méthode est utilisée par Léonard dans les tentatives, plus ou moins réussies, de construction des autres solides semi-réguliers présents dans ce folio72, dont certains ne sont contenus ni dans les manuscrits ni dans l’édition du De divina proportione.

Analyses géométriques récentes

À la marge de cette reconstruction méthodologique, sur laquelle subsistent peu de doutes, il nous semble utile de mettre en évidence les résultats de certaines études relativement récentes qui ont montré comment le thème reste ouvert à d’ultérieures considérations. Il s’agit en particulier d’études qui ont identifié une série d’erreurs géométriques dans les dessins des planches du De divina proportione, dont certaines pourraient avoir des implications dans la reconstruction de l’histoire de ces illustrations.

Par exemple, une étude conduite par le mathématicien et sculpteur hollandais Rinus Roelofs73 montre que, dans le dessin du rhombicuboctaèdre élevé vide (« vigintisex basium abscisum elevatum vacuum »), la pyramide inférieure présente une base quadrangulaire, alors qu’elle devrait être triangulaire. En outre, les bases de certaines des pyramides adjacentes, qui devraient être quadrangulaires, semblent triangulaires. Cela est vrai pour l’ensemble des trois versions, ce qui signifie que l’erreur se trouvait certainement déjà dans le carton original dont toutes dérivent.

De même, dans toutes les versions du dessin de l’icosidodécaèdre élevé vide (« duodecedron abscisus elevatus vacuus »), il y a des problèmes dans la représentation de la pyramide mise immédiatement en dessous de celle frontale à base pentagonale : il manque certaines lignes de bord, mais différentes entre les trois versions.

La version élevée vide du cuboctaèdre (« exacedron abscisus elevatus vacuus »), quant à elle, présente des problèmes dans sa construction géométrique : les bords de la face triangulaire qui se trouve sur la partie postérieure du solide, au lieu d’être cachés derrière les bords des faces qui sont devant, passent sur un plan plus avancé par rapport à l’observateur quand ils rejoignent les sommets supérieurs externes des pyramides triangulaires.

Dans d’autres contextes, ce type d’erreur s’explique facilement étant donnée la complexité des géométries. Au folio 518r. du Codex Atlanticus74, par exemple, on voit un icosaèdre qui semble avoir treize sommets75. Dans les carnets de Léonard, des imprécisions de la sorte sont relativement communes, étant donné qu’ils ne sont pas destinés à être publiés. On peut donc imaginer que, au moins pour les figures plus les complexes, l’usage d’un perspectographe n’a pas empêché des erreurs, même pour la main et l’œil d’un expert tel que Léonard de Vinci. Une autre hypothèse serait que les dessins de Léonard de Vinci aient été parfaitement justes, et que les erreurs se soient glissées lors du transfert de ces dessins sur les codex. Comme pour le portrait d’après nature, les figures les plus complexes ont pu mettre en difficulté celui qui a transféré le dessin – peut-être Léonard lui-même, si l’on accepte l’hypothèse qu’il soit intervenu personnellement sur le Codex de Milan.

Ce problème de la propagation des erreurs est assez intéressant : on en trouve un autre exemple dans une marqueterie raffinée dédiée aux mathématiques, qui décore la sacristie de l’église Santa Maria in Organo, à Vérone (fig. 10), réalisée par Fra Giovanni da Verona entre 1519 et 152376. Elle représente une série d’objets contenus dans une armoire, un thème iconographique relativement populaire à l’époque puisqu’on le voit également au Palais Ducal d’Urbino et au Palais Ducal de Gubbio. Ce répertoire inclut généralement des sphères armillaires, des compas et d’autres objets appréciés par les intellectuels de l’époque.

Sur le panneau de Vérone, une sphère polyédrique de Campanus est reproduite dans le haut de la scène77 ; en dessous se trouve un icosaèdre et, encore en dessous, un icosaèdre tronqué. Cette dernière figure a été reprise, probablement, de l’illustration de Léonard de Vinci du Compendium de divina proportione dans la version milanaise, étant donné qu’elle reproduit une erreur78 : la face la plus basse, celle sur laquelle repose le solide, est de forme carrée, comme dans le Codex de Milan79 (fig. 11-12). Or, normalement, l’icosaèdre tronqué n’est composé que de faces hexagonales et pentagonales80. Notons également que toutes les trois figures de Fra Giovanni proviennent du De divina proportione. Mais si la sphère polyédrique de Campanus et l’icosaèdre sont représentés avec une orientation différente par rapport à ceux de l’œuvre de Pacioli (fig. 13-14), l’icosaèdre tronqué est exactement dans la même position que dans le De divina proportione, ce qui pourrait confirmer qu’il provient bien de cette source81.

Le dernier exemple que je voudrais donner, pour conclure ce bref article, concerne une erreur d’une autre nature, commise cette fois par Pacioli, qui nous ramène en quelque sorte à la question initiale des deux approches alternatives possibles : l’une purement géométrique, l’autre qui prévoit la construction des modèles. Dans la section LII du De divina proportione, à propos de l’icosidodécaèdre élevé, Pacioli affirme que le sommet d’une des pyramides à base pentagonale et les sommets des cinq pyramides à base triangulaire qui entourent la première, reposent tous sur un même plan82. Cette affirmation n’est pas correcte : une reconstruction en trois dimensions du solide montre clairement que la pyramide pentagonale au centre dépasse légèrement du plan qui passe par les cinq autres (fig. 15).

On pourrait en déduire que Pacioli n’avait pas de modèle du solide à sa disposition pour vérifier son affirmation83. Or, la partie finale du chapitre de Pacioli semble faire référence à un modèle physique qui, observé accroché en l’air, ne donnerait pas, à son avis, l’impression de jouir de cette propriété. Il affirme tout de suite après qu’une vérification doit être réalisée à l’aide d’instruments de mathématiques (« algebra e almucabala »), ce qui permettrait au mathématicien de relever l’erreur84.

S’agit-il donc de mauvais calculs ? Il est plus probable que Pacioli n’ait jamais effectué les vérifications mathématiques et que son affirmation se serait donc fondée sur un modèle construit peu soigneusement. Par ailleurs, un icosidodécaèdre élevé de dimensions telles à pouvoir s’inscrire dans une sphère de 50 cm de diamètre aurait présenté une différence de hauteur entre les sommets des pyramides de 5 mm environ, ce qui est peut-être trop peu pour être visible sur un modèle construit à l’aide des instruments de l’époque.

La manière dont Léonard de Vinci a exécuté les dessins du Compendium de divina proportione pour Luca Pacioli est donc, aujourd’hui encore, au centre d’un débat intéressant et animé. Ce qui semble toutefois se dégager clairement, c’est la place de ces illustrations à la frontière multiforme entre le dessin technique et le dessin purement artistique. Indépendamment de la manière dont elles ont été créées, il est en effet incontestable que ces images représentent une contribution importante à l’histoire du dessin : en elles, les concepts mathématiques et le travail artistique ont été indissolublement fusionnés, donnant naissance à un genre figuratif inédit. Devenus par la suite un paradigme de la manière dont l’art et la science peuvent interagir, ces « portraits géométriques » ont inspiré de nombreux artistes au cours des siècles85.